La enseñanza de las matemáticas en Singapur, conocida como “Matemáticas Singapur”, está basada en ideas clásicas de Didáctica de las Matemáticas, bien conocidas desde hace al menos 50 años. Las más importantes son:
- El aprendizaje en tres etapas (Jerome Brunner). Para que los alumnos comprendan un concepto matemático, es necesario que pasen por estas tres etapas: una primera, concreta, con materiales manipulativos, una segunda, visual, basada en representaciones gráficas, y una tercera, la simbólica, las “matemáticas tradicionales”.
- La comprensión de los conceptos y el aprendizaje de los procedimientos deben trabajarse en paralelo (Richar Skemp). Entender lo que estamos haciendo, y por qué funcionan los procedimientos matemáticos (ya sea sumar con “llevadas” en 1ºEP, o resolver ecuaciones de 2º grado en ESO) es la mejor forma de conseguir un aprendizaje significativo, que los alumnos puedan usar en el futuro, conectar con otras áreas de las matemáticas, y transferir a contextos y situaciones diferentes.
- Es conveniente usar diferentes representaciones de los conceptos, y estudiar diferentes formas de resolver un problema (Zoltan Dienes, George Pólya).
- El andamiaje y la zona de desarrollo próximo (Lev Vygotski). Para que los alumnos puedan comprender lo que hacen las secuencias didácticas se deben secuenciar, de manera que las actividades que se proponen en cada momento estén en la zona de desarrollo próximo de los alumnos, que son aquellas actividades muy cercanas a lo que los alumnos ya han comprendido.
El sentido numérico se suele definir como la capacidad de comprender los números y sus representaciones, y ser capaz de calcular de manera flexible con ellos. Es fundamental para progresar de forma adecuada en el estudio de la aritmética.
Una de las herramientas más potentes de la metodología Singapur son las descomposiciones numéricas, que llamaremos números conectados.
En la imagen, vemos la representación de una descomposición del 7, que resumen la situación partes/total de la imagen, y que es una manera muy eficiente de resumir estos cuatro hechos numéricos.
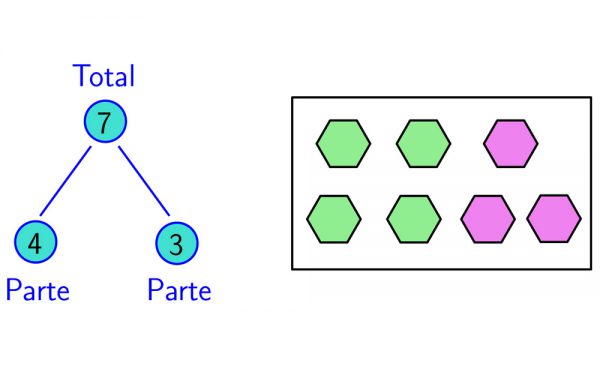
En la siguiente imagen vemos algunas situaciones en las que los números conectados se pueden usar para calcular, con estrategias que se pueden describir como “cálculo razonado”.
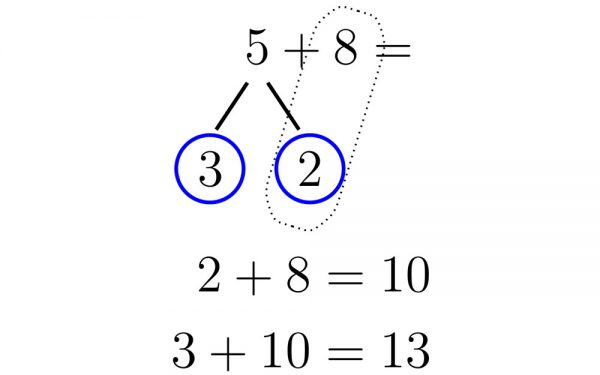
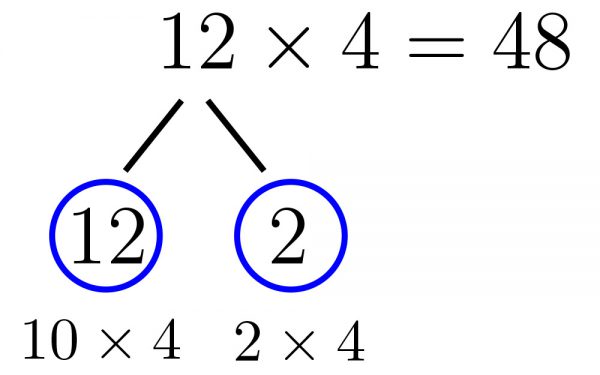
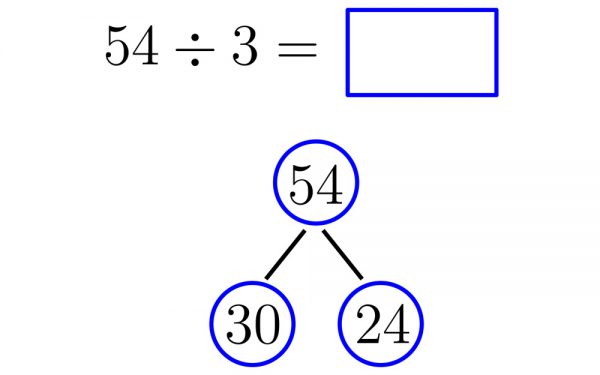
Otra herramienta tan importante como la anterior es el modelo de barras.
En este modelo se representan, usando rectángulos, las cantidades que aparecen en un problema, y las relaciones entre ellas. Se trata de una herramienta de pensamiento visual, que es de gran ayuda en la resolución de problemas.
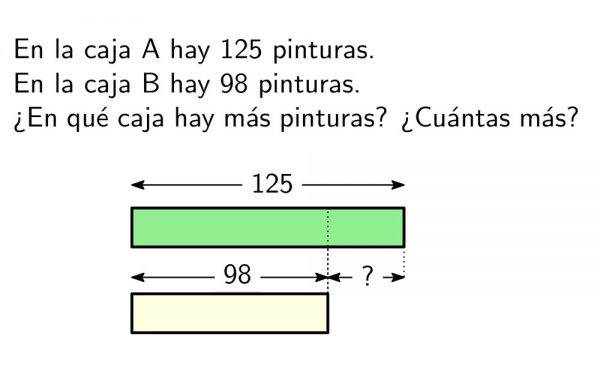
En la siguiente imagen podemos ver dos problemas que se pueden resumir en situaciones de partes/total:


A continuación vemos un ejemplo de un modelo que representa una situación de comparación:
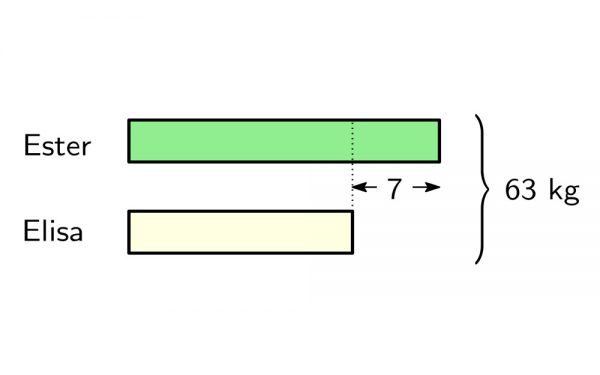
El modelo significa un paso de abstracción importante cuando se introduce (en 2ºEP). Una vez comprendido, permite abordar ya al final de ese curso problemas como este:
- Ester pesa 7 kg más que su amiga Elisa. Si entre las dos pesan 63 kg, ¿cuánto pesa cada una?
Para terminar, dos problemas propuestos, ya sin la solución, que muestran las posibilidades del modelo a lo largo de la primaria. En primer lugar, un ejemplo de cómo el modelo de barras es una excelente herramienta para la introducción del pensamiento algebraico.
- Pablo tiene la mitad de dinero que Laura, y Miguel tiene 7 € menos que Laura. Si entre los tres tienen un total de 233 €, ¿cuánto dinero tiene cada uno?
Este último es un ejemplo de aplicación del modelo en los problemas en los que intervienen fracciones. Está tomado de una prueba final de primaria de Singapur que se Pconsultar, competa, en estos enlaces:
• Prueba primaria singapur 1
• Prueba primaria singapur 2
- Lisa y Pablo hicieron tarjetas durante dos días. El sábado, Lisa hizo 19 tarjetas más que Pablo. El domingo, Lisa hizo 20 tarjetas, y Pablo hizo 15. Al acabar los dos días, Lisa hizo 3/5 del total de las tarjetas. ¿Cuántas tarjetas hizo Pablo?
Seguiremos pensando infinito, seguiremos formando e informando.
Autor: Pedro Ramos Alonso, Profesor titular del área de matemática aplicada en el Departamento de Matemáticas de la Universidad de Alcalá.